Расчет на продавливание ростверка угловой сваей

Как правильно расчитать ростверк на продавливание угловой сваей

Страница 1 из 2

1

2

>

DWG 2007

ростверк.dwg (61.0 Кб, 1919 просмотров)

Вложения

1xxx.pdf (208.6 Кб, 505 просмотров)

Спасибо за пример.
Если считать верхнюю сваю по СП 52-101 необходимо учитывать момент от расцентровок, в этом случае контуром продавливания будет прямая с очень маленьким моментом сопротивления и ростверк не проходит. Если по пособию по ростверкам и по СниП 2.03.01 то моменты не возникают и ростверк проходит.
Нужно ли учитывать момент от расцентровки?

В примере значение с принимают равным h0*04. В пособии не сказано что ожно увеличивать

SergeyKonstr

Посмотреть профиль

Найти ещё сообщения от SergeyKonstr

SergeyKonstr

Посмотреть профиль

Найти ещё сообщения от SergeyKonstr

С4 с двумя вариантами контуров. 1-ый не более с=ho. 2-ой по граням стен.

Значит С1, С2, С3 продавливания нет? А если С1 и С2 стоят точно по грани то будет 1 контур по грани стен?

Для С4:
1-ый не более с=ho/2?

С оно и есть с-длина проекции наклонного сечения.
если с=0, то отношение h0/c=бесконечности и на длине одной составляющей периметра среза сопротивление не более =2,5*Rbt*u1*h0 (п.8.1.33 СП 63).
если с=h0, то отношение h0/c=1 и на длине другой составляющей периметра среза сопротивление не более =1,5*Rbt*u2*h0 (п.8.1.33 СП 63).
если с более h0, и отношение h0/c менее 1/3 и на длине другой составляющей периметра среза сопротивление не более =0,5*Rbt*u2*h0 (п.8.1.33 СП 63).

Давится две грани с с=0.

Лучше круг. попер. сечение сделайте равновеликим квадратным.

SergeyKonstr

Посмотреть профиль

Найти ещё сообщения от SergeyKonstr

Возможно сейчас такую тупость скажу. В СП принимают расчетный контур на расстоянии h0/2,

а для С4
при 1)С=h0
и по 2)граням стен
какая величина расчетного контура будет, что то не улавливаю

SergeyKonstr правильно ли посчитаны контуры на миниатюре? Не пойму откуда h0/2 в СП (центр тяжести проекции наклонного сечения?), нужно ли для определения расчетного контура проекцию наклонной трещины С делить на 2.

Первый контур не правильно.
Второй правильно.

Нужно конечно.
Смотрите структуру формулы (14) Пособия по проектированию ростверков свай. ф-тов под колонны. М, 1985.

Вложения

23.docx (1.85 Мб, 33 просмотров)

SergeyKonstr

Посмотреть профиль

Найти ещё сообщения от SergeyKonstr

SergeyKonstr

Посмотреть профиль

Найти ещё сообщения от SergeyKonstr

Остается два небольших вопроса
1) вы говорите:
если с=0, то отношение h0/c=бесконечности и на длине одной составляющей периметра среза сопротивление не более =2,5*Rbt*u1*h0 (п.8.1.33 СП 63).
если с=h0, то отношение h0/c=1 и на длине другой составляющей периметра среза сопротивление не более =1,5*Rbt*u2*h0 (п.8.1.33 СП 63).
если с более h0, и отношение h0/c менее 1/3 и на длине другой составляющей периметра среза сопротивление не более =0,5*Rbt*u2*h0 (п.8.1.33 СП 63)

По СП формула (8.88) предельное усилие воспринимаемое бетоном Fb.ult=Rbt*Ab, а не 1,5*Rbt*u2*h0 ? Как же все таки считать предельное усилие воспринимаемое бетоном для найденного контура

2) проверка прочности незамкнутого расчетного сечения при действии силы F приложенной с эксцентриситетом.

В пособии говорится что сила F принимается за вычетом нагрузок приложенных к противоположной грани плиты в пределах площади превышающей размер площадки опирания на h0. По моим схемам не понятно какую величину вычитать из F возникающей в свае при нагрузке от стен. Да у меня там вродебы и нет нагрузок.

Хотя расчет приблизительный при полной F без вычета сечения не хватает.

Эксцентриситет продольной силы относительно центра тяжести расчетного контура вдоль оси X:
eox = abs(yo-yF) = abs(0,42563-0,25) = 0,17563 м = 17,56 см .
Эксцентриситет продольной силы относительно центра тяжести расчетного контура вдоль оси Y:
eoy = abs(xo-xF) = abs(0,42563-0,25) = 0,17563 м = 17,56 см .
Предельное усилие, воспринимаемое бетоном:
Fb, ult = min(Rbt u2 ho ; Rbt ho /(1/u1+eox/Wbx) ; Rbt ho /(1/u1+eoy/Wby)) =
= min(0,675 · 2,54 · 0,435;0,675 · 0,435/(1/1,135+0,17563/0,08944);0,675 · 0,435/(1/1,135+0,17563/0,08944)) = 0,10322 МН = 10,53 тс .
F = 0,25497 МН = 26 тс r Fb, ult = 0,10322 МН = 10,52551 тс (247,01889% от предельного значения) — требуемое условие не выполняется ! (формула (8.87); п. п. 8.1.47 ). Помоему где то ошибка

Пример 4. Расчет плитного ростверка на продавливание в месте опирания на сваю

Плита ростверка опирается на сваи. Сваи собраны в кусты в месте опирания колонн, сама же колонна опирается в пролете между сваями. Требуется выполнить расчет плиты ростверка на продавливание в месте опирания на сваю согласно п. 3.96 Пособия по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры к СНиП 2.03.01-84.

Дан ростверк на сваях, шаг колонн 5х5 м, в районе каждой колонны куст из четырех свай, расстояние между сваями 1 м (по оси У) и 1,6 м (по оси Х), колонна – посередине. Требуется выполнить расчет ростверка на продавливание в районе заштрихованной сваи. Толщина плиты ростверка 500 мм, расстояние от нижней грани плиты до оси рабочей арматуры 50 мм, бетон класса В25 (Rbt = 9.7 кг/см² при коэффициенте условий работы 0,9), площадь сбора нагрузки от ростверка, приходящаяся на колонну – 2,5х2,5 м², временная нагрузка от пола 1-го этажа 400 кг/м², постоянная нагрузка (без учета собственного веса плиты) 300 кг/м²; сечение колонны 300х300 мм; нагрузки от колонны на ростверк N=400 т, Мх = 50 т∙м, Му = 36 т∙м; диаметр сваи 400 мм.

Оптимально для расчета на продавливание брать наибольшую нагрузку на сваю, полученную в результате расчета ростверка или всего здания в целом. Но предположим, что у нас нет таких результатов, и соберем нагрузку на сваю для имеющихся исходных данных.

Какие вертикальные нагрузки придутся на сваю? Все равномерно-распределенные нагрузки (вес ростверка, временная и постоянная нагрузка на ростверк), взятые с расчетной площади. Расчетную площадь (показана на рисунке синим пунктиром) определить легко: между нашей сваей и всеми соседними проводим осевые линии (ровно посредине между сваями) – нагрузка от половины пролета придется на нашу сваю, от другой половины – на соседнюю. В итоге, мы получаем квадрат сбора нагрузки 2,5х2,5 м.

Найдем вертикальную нагрузку, действующую на сваю от ростверка:

2185∙2,5∙2,5 = 13656 кг = 14 т.

Еще у нас есть колонна, которая стоит на пересечении двух осей. Вертикальная нагрузка от этой колонны N поровну делится между четырьмя сваями.

Вертикальная нагрузка на сваю от колонны будет равна:

Также у нас есть два момента от колонны, каждый из которых раскладывается на пару сил: М = N∙L. От каждого из моментов на сваю может приходиться вертикальная сила, которую нужно вычислить.

В нашем случае нагрузка на одну сваю равна N/2, т.к. свай всего четыре. Значит, нагрузку на сваю можно найти по формуле N/2 = 0.5(M/L)

В направлении действия момента Мх = 50 т∙м расстояние между сваями L=1,6 м. Найдем нагрузку на нашу сваю от момента, направленную вниз и равную:

Nх/2 = 0.5(50/1,6) = 16 т.

В направлении действия момента Му = 36 т∙м расстояние между сваями L=1,0 м. Найдем нагрузку на нашу сваю от момента, направленную вниз и равную:

Nу/2 = 0.5(36/1,0) = 18 т.

Найдем суммарную вертикальную нагрузку на сваю:

F = 14 + 100 + 16 + 18 = 148 т.

Реакция сваи, направленная вверх, на которую мы будем проверять наш ростверк на продавливание, равна нагрузке F = 148 т, только направлена она вверх.

Так как свая круглая, пирамида продавливания у нас представляет собой усеченный конус с двумя круглыми основаниями. Определяем рабочую высоту сечения плиты h₀ = 500 – 50 = 450 мм. Прорисовываем «пирамиду» и видим, что колонна не попала в площадь большего круга. Если бы колонна оказалась в пределах «пирамиды» продавливания, то размеры конуса пришлось бы уменьшить до грани колонны (как на рис. 65б пособия – только на рисунке конус разрастается сверху вниз и ограничен внизу, а у нас наоборот).

Определим периметры оснований пирамиды:

3,14∙0,4 = 1,3 м – периметр меньшего основания;

3,14∙1,3 = 4,1 м – периметр большего основания.

Найдем среднеарифметическое значение периметров:

Определим, чему равна правая часть уравнения (200):

1,0∙9,7∙10∙2,7∙0,450 = 118 т.

Проверим, выполняется ли условие (200):

F = 148 т > 118 т – условие не выполняется, необходимо делать проверку ростверка с дополнительным армированием.

Зададимся поперечной арматурой в ростверке, работающем на продавливание: d10 мм с шагом 100х100 мм.

В пределах конуса продавливния разместилось 124 стержня Asw = 124∙0,785 = 97,34 см².

Вычислим Fsw (здесь 175 МПа = 1750 кг/см² — предельное напряжение в поперечных стержнях):

Fsw = 1750∙97,34 = 170345 кг = 170,3 т 0,5Fb:

Расчет на продавливание ростверка угловой сваей

Расчет ростверков на продавливание угловой сваей проводится из условия

где F_ai — расчетная нагрузка на угловую сваю с учетом моментов в двух направлениях, включая влияние местной нагрузки (например, от стенового заполнения), кН; h₀₁ — рабочая высота сечения на проверяемом участке, равная расстоянию от верха свай до верхней горизонтальной грани плиты ростверка или его нижней ступени; u_i — полусумма оснований i-й боковой грани фигуры продавливания высотой h₀₁, образующейся при продавливании плиты ростверка угловой сваей, м; — коэффициент, определяемый по табл. 7 в зависимости от:

В преобразованном виде формула будет иметь вид

где b₀₁; b₀₂ — расстояния от внутренних граней угловых свай до наружных граней плиты ростверка, м (рис. 13, 14); с₀₁,с₀₂ — расстояния от внутренних граней угловых свай до ближайших граней подколонника ростверка или до ближайших граней ступени при ступенчатом ростверке, м; ₁, ₂— значения этих коэффициентов принимаются по табл. 7 [9].

1. При h₁/c₀₁ и h1/c₀₂, меньшем 1, коэффициенты ₁ и ₂ принимаются соответственно такими же, как и при h₀₁/c_oi=1, то есть равными 0,6; при этом с₀₁ и с₀₂ принимаются равными h₁.

2. При h₁/c₀₁ и h₁/c₀₂, большем 2,5, коэффициенты ₁ и ₂ принимаются равными 1, а величины с₀₁ и c₀₂ равными 0,4h₁.

3. В тех случаях, когда угловая свая в ростверках с подколонником по проекту заходит в плане за обе грани подколенника на 50 мм и более, проверка на продавливание плиты ростверка угловой сваей не проводится.

Расчет средней колонны

при h = 0,75 м, h₀₁ = 0,75-0,5 = 0,7 м

Рис. 13. Схема продавливания ростверка угловой сваей

класса бетона В25

R_bt = 1,05*10 3 *0,9 = 0,945*10 3 кПа

при h = 0,9 м, h₀₁ = 0,9-0,5 = 0,85 м

класса бетона В25

R_bt = 1,05*10 3 *0,9 = 0,945*10 3 кПа

Расчет средней колонны

Рис. 14. Схема продавливания ростверка угловой сваей

при h = 0,9 м, h₀₁ = 0,9-0,5 = 0,85 м

класса бетона В15

R_bt = 0,75*10 3 *0,9 = 0,675*10 3 кПа

при h = 1,05 м, h₀₁ = 1,05-0,5 = 1,00 м

класса бетона В15

R_bt = 0,75*10 3 *0,9 = 0,675*10 3 кПа

Расчет ростверка на изгиб

Расчет прочности ростверков на изгиб проводится в сечениях по граням колонны, а также по наружным граням подколонника ростверка или по граням ступеней ростверка.

Расчетный изгибающий момент для каждого сечения определяется как сумма моментов от реакций свай (от расчетных нагрузок на ростверк) и от местных расчетных нагрузок, приложенных к консольному свесу ростверка по одну сторону от рассматриваемого сечения:

где M_xi, M_yi — изгибающие моменты в рассматриваемых сечениях; F_i -расчетная нагрузка на сваю, нормальная к площади подошвы ростверка; x_i, у_i — расстояния от осей свай до рассматриваемого сечения.

Площадь сечения арматуры, параллельной стороне а_p , на всю ширину ростверка определяется:

в сечении 2-2 по грани ступени (подколонника)

где A_s — площадь поперечного сечения арматуры, должна приниматься не менее минимального процента армирования для железобетонных конструкций м = 0,05 %.

Площадь сечения арматуры, параллельной стороне b_p, на всю длину ростверка определяется:

в сечении 4-4 по грани ступени (подколонника)

где M_y1,M_y2 — изгибающие моменты на всю ширину ростверка соответственно в сечениях 1 — 1 и 2 — 2; М_x1, М_x2 — изгибающие моменты на всю длину ростверка соответственно в сечениях 3-3 и 4-4; h₀₂ — рабочая высота ростверка в сечениях 1-1 и 3-3; h₀₁ — рабочая высота ростверка в сечениях 2-2 и 4-4; R_s — расчетное сопротивление арматуры (табл. 22)[5]; н- коэффициент, определяемый по табл. 8 [9] в зависимости от коэффициента, рассчитываемого для:

где R_b — расчетное сопротивление бетона осевому сжатию (табл. 12)[5]; а_p, b_p — размеры подошвы ростверка; а₁, b₁ — размеры сечения стаканной части ростверка.

Сетки рабочей арматуры следует конструировать в соответствии с требованиями [6].

Расчет средней колонны

Рис. 15. Расчетная схема при определении арматуры подошвы ростверка

для класса бетона В25

R_b = 14,5*10 -1 *0,9 = 13,05*10 -1 кН/см 2

Принимаю арматуру, параллельную стороне а_p, длиной l = 2800 мм ф = 20 класса АIII с шагом S=100 мм А_s f = 3,142 см 2 .

Принимаю арматуру, параллельную стороне b_p, длиной l = 2000 мм ф = 20 класса АIII с шагом S=100 мм А_s f = 3,142 см 2 .

Расчет средней колонны

Рис. 16. Расчетная схема при определении арматуры подошвы ростверка

для класса бетона В15

R_b = 8,5*10 -1 *0,9 = 7,65*10 -1 кН/см 2

Принимаю арматуру, параллельную стороне а_p, длиной l = 1600 мм ф = 10 класса АIII с шагом S=150 мм А_s f = 1,131 см 2 .

Принимаю арматуру, параллельную стороне b_p, длиной l = 1600 мм ф = 12 класса АIII с шагом S=130 мм А_s f = 1,539 см 2 .

Расчет ростверков на продавливание угловой сваей

2.9. Расчет ростверков на продавливание угловой сваей производится из условия

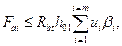(12)

где F_ai — расчетная нагрузка на угловую сваю с учетом моментов в двух направлениях, включая влияние местной нагрузки (например, от стенового заполнения);

h₀₁ — рабочая высота сечения на проверяемом участке, равная расстоянию от верха свай до верхней горизонтальной грани плиты ростверка или его нижней ступени.

и_i — полусумма оснований i-й боковой грани фигуры продавливания высотой h₀₁, образующейся при продавливании плиты-ростверка угловой сваей;

b_i — коэффициент, определяемый по формуле

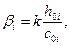(13)

здесь k — коэффициент, учитывающий снижение несущей способности плиты ростверка в угловой зоне.

В преобразованном виде формула (12) будет иметь вид

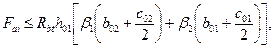(14)

где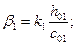

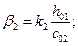
b₀₁; b₀₂ — расстояния от внутренних граней угловых свай до наружных граней плиты ростверка (черт. 6);

c₀₁; c₀₂ — расстояния от внутренних граней угловых свай до ближайших граней подколенника ростверка или до ближайших граней ступени при ступенчатом ростверке;

b₁ и b₂ — значения этих коэффициентов принимаются по табл. 1.

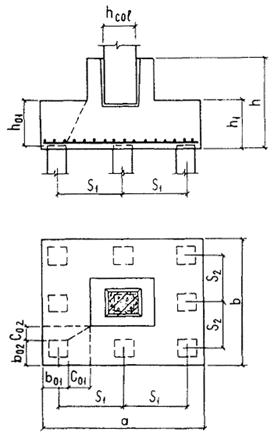
Черт. 6. Схема продавливания ростверка угловой сваей

h01 ci	bi	h01 ci	bi	h01 ci	bi	h01 ci	bi
0,6	1,4	0,765	1,8	0,887	2,2	0,968
1,05	0,622	1,45	0,782	1,85	0,9	2,25	0,974
1,1	0,645	1,5	0,8	1,9	0,912	2,3	0,98
1,15	0,666	1,55	0,815	1,95	0,92	2,35	0,986
1,2	0,688	1,60	0,832	0,932	2,40	0,991
1,25	0,709	1,65	0,845	2,05	0,941	2,45	0,996
1,3	0,728	1,7	0,86	2,1	0,951	2,5
1,35	0,746	1,75	0,875	2,15	0,96

Примечания: 1. Пр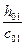и и 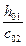, меньшем 1, коэффициенты b₁ и b₂ принимаются соответственно такими же, как и при 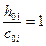, то есть равными 0,6; при этом c₀₁ и с₀₂ принимаются равными h₀₁.

Пр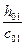и и 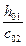, большем 2,5, коэффициенты b₁ и b₂ принимаются равными 1, а величины c₀₁ и с₀₂ равными 0,4h₀₁.

2. В тех случаях, когда угловая свая в ростверках с подколенником по проекту заходит в плане за обе грани подколенника на 50 мм и более, проверка на продавливание плиты ростверка угловой сваей не производится.

Расчет железобетонных ростверков

В зависимости от условий работы железобетонные ростверки подразделяются на ленточные ростверки под кирпичные и крупноблочные стены, ленточные ростверки под крупнопанельные стены, безростверковые свайные фундаменты под крупнопанельные стены, в которых в качестве ростверка работает панель здания, и на плитные ростверки под колонны каркасных зданий.

Методика расчета ленточных ростверков и безростверковых свайных фундаментов детально изложена в прил.9, 10, 12 Руководства [3]. В приложении 11 того же Руководства изложены основные положения по расчету ростверков под колонны, на основании которых расчет ростверка производится в следующем порядке: на продавливание колонной; на продавливание угловой сваей; на поперечную силу в наклонных сечениях; на изгиб; на местное сжатие под торцом сборной колонны; на прочность стаканной части; на раскрытие трещин.

На продавливание колонной ростверк (рис.2.2.) рассчитывается по формуле:

где N – расчетная продавливающая нагрузка, равная удвоенной сумме реакций всех свай, расположенных с одной наиболее нагруженной стороны от оси колонны за пределами нижнего основания пирамиды продавливания; подсчитывается от усилий, действующих в плоскости верха фундамента; h – рабочая высота ростверка, принимаемая от верха нижней рабочей арматурной сетки до дна стакана при сборной колонне и до верха ростверка при монолитной и стальной колонне; b_c, d_c – ширина и высота сечения колонны; с₁, с₂ – расстояния от соответствующих граней колонн до внутренних граней каждого ряда свай, принимаемые от 0,4h до h; α₁, α₂ – безразмерные коэффициенты, равные α_i=h/c_i и принимаемые от 2,5 до 1; R_bt – расчетное сопротивление бетона осевому растяжению.

Для стаканного ростверка при е > 0,5 максимальный момент в плоскости верха ростверка допускается принимать:

При продавливании колонной составных ростверков их рабочая высота принимается как для цельных ростверков той же высоты.

Минимальная толщина дна стакана принимается равной 40 см.

Расчет на продавливание угловой сваей плитной части ростверка (рис.2.2.) производится по формуле:

где N_p – расчетная нагрузка на угловую сваю, подсчитанная от нагрузок, действующих в плоскости низа ростверка; h₂ – высота ступени ростверка от верха сваи; b₀₁, b₀₂ – расстояния от внутренних граней угловой сваи до ближайших наружных граней ростверка;

с₀₁, с₀₂ – расстояния от внутренних граней свай до ближайших граней ступени ростверка или подколонника, принимаемые от 0,4h₂ до h₂; β₁, β₂ – безразмерные коэффициенты, принимаемые в зависимости от отношения h₂/с:

h2/с	βi	h2/с	βi	h2/с	βi	h2/с	βi
1,0 1,1 1,2 1,3	0,60 0,65 0,69 0,73	1,4 1,5 1,6 1,7	0,76 0,80 0,83 0,86	1,8 1,9 2,0 2,1	0,89 0,91 0,93 0,95	2,2 2,3 2,4 2,5	0,97 0,98 0,99 1,00

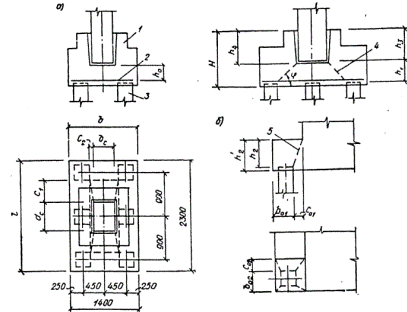
Рис.2.2. Свайный фундамент со стаканным ростверком

а – общий вид;

б – расчетная схема ступени;

1 – ростверк; 2 – арматура;

3 – свая; 4 – пирамида продавливания колонной;

5 – то же, угловой сваей

На поперечную силу в наклонных сечениях ростверк рассчитывается по формуле:

где ΣN_p – расчетная нагрузка на все находящиеся за пределами наклонного сечения сваи, которая определена от нагрузок, действующих в плоскости низа ростверка; b – ширина ростверка (для ступенчатых ростверков с разной шириной ступеней принимается приведенная величина b`); h₀₁ – рабочая высота рассматриваемого сечения ростверка; m – безразмерный коэффициент, отвечающий условию 0,75R_btbh≤k_зR_btbh 2 /c≤2,5R_bth (здесь k_з=1,5 принят как для сплошных плит) и принимаемый в зависимости от отношения h/c:

h/с	m	h/с	m	h/с	m	h/с	m	h/с	m
1,67 1,65 1,60 1,55 1,50	2,50 2,48 2,40 2,33 2,25	1,45 1,40 1,35 1,30 1,25	2,18 2,10 2,03 1,95 1,88	1,20 1,15 1,10 1,05 1,00	1,80 1,73 1,65 1,58 1,50	0,95 0,90 0,85 0,80 0,75	1,43 1,35 1,28 1,20 1,13	0,70 0,65 0,60 0,55 ≤0,50	1,05 0,98 0,90 0,83 0,75

Расчетный изгибающий момент определяется в сечениях по граням колонн и ступеней от расчетных нагрузок на сваи, умноженных на расстояние от оси свай до соответствующих граней ступени или колонны.

При действии на сваю расчетных выдергивающих нагрузок ростверк должен рассчитываться на изгиб от действия отрицательных реакций свай.

Расчет ростверков на местное сжатие (смятие) под торцом сборной колонны выполняется в соответствии со СНиП 2.02.01-83 по формуле:

где N – расчетная нагрузка, действующая в сечении колонны на уровне верха ростверка;

R_bt – расчетное сопротивление бетона осевому сжатию; А_с – площадь сечения колонны (для двухветвевой колонны, у которой отсутствует распорка понизу, площадь ветвей колонны).

Расчет продольной арматуры стаканной части ростверка производится в соответствии с указаниями СНиП II-21-75 на внецентренное сжатие коробчатого сечения в плоскости заделанного торца колонны. Аналогично рассчитывается подколонник под стальную и монолитную железобетонную колонну.

Минимальные размеры сечения продольной арматуры стенок стакана или подколонника составляют 0,05% расчетных размеров сечения бетона. Поперечное армирование стенок стакана определяется по расчетному моменту, действующему относительно торца колонны и вычисляемому по формулам:

при d_с/2 > е ≥ d_s/6

при е ≥ d_с/2

где е=М/N_р – эксцентриситет приложения внешних нагрузок; М, N_р, Q – расчетные нагрузки, действующие на отметке верха стакана; d_c, h_c – длина стороны сечения и глубина заделки колонны.

Площадь сечения поперечной арматуры определяется по формуле

где R_s – расчетное сопротивление арматуры растяжению; z_i – расстояние от каждой сетки до торца колонны.

При е ≤ d_с/6 поперечное армирование стенок стакана выполняется конструктивно двумя сетками. Стенки стакана допускается не армировать, если отношение толщины стенок стакана к высоте его уступа или к глубине стакана более 0,75.

При применении ростверков в агрессивной среде их следует рассчитывать по раскрытию трещин согласно указаниям СНиП 2.02.01-83.

Пример 2.2. Рассчитать ростверк размером в плане 240Х150 см при размере подколонника 120Х90 см из бетона марки М200. Размеры колонны d_с=60 см; b_с=40 см. Расчетная нагрузка на ростверк N = 4 200 кН; М = 250 кН·м; F_h = 60 кН; заделка колонны h_з=85 см, глубина стакана h₄=90 cм. Куст из шести свай сечением 30Х30 см, расстояние между сваями l_i=90 см (см. рис.2.2).

Решение. Принимаем конструктивно высоту ростверка h=h₄+45 см=135 см, а=7 см. Расчетные усилия в сваях от нагрузок на уровне верха ростверка

Расчетное продавливающее усилие, действующие на ростверк,

ΣN_pi = 770·4 + 700·2 = 4480 кН.

Расчетное продавливающее усилие, воспринимаемое ростверком, определяется по формуле (2.4). Принимаем h=38 см. Тогда

N = 2·7,5·3,8[1(40+15) + 2,5(60+38)] = 1710 кН,

где с₁=45 см; с₂=10 см; α₁=38/45 ΣN_pi=4480 кН.

Общая высота ростверка из бетона М300 по условию продавливания колонной h_c=h+a+h₄= =68+7+90=165 cм. Вес ростверка и грунта на его обрезах G=120 кН. Расчетные усилия в сваях от нагрузок на уровне низа ростверка с учетом веса ростверка и грунта на обрезах:

Принимаем высоту ступени ростверка h`=75 см и проверяем прочность ступени на продавливание угловой сваей, заделанной в ростверк на 5 см;

N_р = 10·70·2·1(45+22/2) = 828 кН > F_υ = 823 кН.

Проверяем высоту ступени по поперечной силе. Для h/с=68/15 > 1,67 находим m=2,5.

Тогда ΣN_p = 2,5·1,50·68·10=2550 кН > 2F_υ = 1646 кН.

Высота ступени h₂=75 см достаточна. Изгибающие моменты относительно граней ступени и колонны соответственно:

М₁ = 2·823·0,3 = 494 кН;

М₂ = 2·823·0,6 = 988 кН.

Требуемая расчетная площадь сечения продольной арматуры класса А-III подошвы ростверка принимается наибольшей из двух:

А₁ = 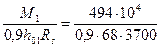= 21,8 см 2 ;

А₂ = 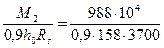= 18,8 см 2 .

Принимаем арматуру 7Ø20 А-III; А_s=21,99 см 2 . Остальные расчеты по армированию ростверка проводятся аналогично.